Interdisziplinäre Forschung in der Deutschdidaktik
«Fremde Schwestern» im Dialog
Zusammenfassung
Leseprobe
Inhaltsverzeichnis
- Cover
- Titel
- Copyright
- Autorenangaben
- Über das Buch
- Zitierfähigkeit des eBooks
- Inhaltsverzeichnis
- Iris Winkler, Frederike Schmidt - Interdisziplinäre Forschung in der Deutschdidaktik. Eine Zwischenbilanz
- Thomas Boyken - Über wissenschaftliche Verwandtschaftsverhältnisse. Versuch einer Einordnung der aktuellen Entwicklungen innerhalb der Deutschdidaktik aus literaturwissenschaftlicher Sicht
- Gerhard Rupp - Fremde und vertraute Schwestern – Konstellationen interdisziplinärer Forschung in der Deutschdidaktik seit den 90er Jahren
- Volker Frederking, Sofie Henschel - Interdisziplinäre Forschung in der Deutschdidaktik am Beispiel des Projekts Literarästhetische Urteils- und Verstehenskompetenz (LUK)
- Katrin Böhme, Petra Stanat, Michael Becker-Mrotzek - Die Entwicklung integrierter Kompetenzstufenmodelle als Ergebnis interdisziplinärer Kooperation
- Ulrike Behrens, Sebastian Weirich - It takes a whole village… Interdisziplinäre Perspektiven bei der Entwicklung eines Testverfahrens zum Zuhören
- Irene Pieper, Florentina Sâmihăian - International Research Cooperation in What Used to Be Called Mother Tongue Education. The Example of LiFT-2
- Iris Winkler, Matthias Heinrich, Astrid Fischer, Ulrike Krause - Multiperspektivität in der Lehrerbildung. Fächerübergreifendes Lernen in der Mathematik- und Deutschdidaktik
- Frederike Schmidt, Barbara Moschner - „Fremde Schwestern“ und „kritische Freundinnen“ – Lehren und Lernen in einem interdisziplinären Promotionsprogramm in der Lehrerbildung
- Thomas Lindauer, Claudia Schmellentin, Anne Beerenwinkel - Sprachbewusster Naturwissenschafts-Unterricht – Werkstattbericht zu einem transdisziplinären Entwicklungsprojekt
Interdisziplinäre Forschung in der Deutschdidaktik. Eine Zwischenbilanz
Abstract Interdisciplinary collaborations have become an established research approach in „Deutschdidaktik“. In this review we discuss the domain specific implications of this fact. Referring to the articles in this volume, we suggest a classification of interdisciplinary research projects that focuses on two main aspects: the synthesis of involved perspectives and the main objective of interest.
1 Ausgangslage
Der vorliegende Band nimmt die Diskussion auf, die im März 2015 auf der Jenaer Tagung „Fremde Schwestern“ im Dialog. Interdisziplinäre Forschung in der Deutschdidaktik begonnen wurde.1 Der Titel der Tagung, der im Untertitel dieses Buches erhalten ist, spielt auf den Beitrag von Ewald Terhart (2002) an. Terhart verweist darin auf das Spannungsverhältnis zwischen Allgemeiner Didaktik und empirischer Lehr-Lern-Forschung und bringt die Beziehung dieser beiden Disziplinen mit dem Bild von den fremden Schwestern auf den Punkt – Schwestern, die sich trotz der Gemeinsamkeiten ihres Forschungsfeldes in ihren wissenschaftstheoretischen Zugriffen auf dieses Feld so grundlegend unterscheiden, dass damit die gegenseitige Verständigung erheblich erschwert ist. Die Fachdidaktik drängt, quasi als dritte „Schwester“, in letzter Zeit verstärkt auf die Bühne, auf der die beiden erstgenannten „Schwestern“ ihr Verhältnis ausfechten; ob in der Rolle der künftigen Integrationsfigur (Terhart 2002, S. 84) oder der zusätzlichen Konkurrentin (Reusser 2008, S. 222), ist noch nicht ausgemacht.
Die Fachdidaktik Deutsch ist von Haus aus ein Hybridfach (vgl. Klein 2010, S. 21f.). Sie ist „inhärent interdisziplinär“ (Lindauer et al., in diesem Band, S. 226) oder, anders gesagt, eine ‚transdisziplinäre Disziplin‘ (Frederking/Henschel, in diesem Band, S. 74); denn sie amalgamiert Elemente zahlreicher Bezugswissenschaften. Man kann anzweifeln, ob die Deutschdidaktik eine eigene Disziplin ist. Sie bildet – auch im Selbstverständnis der meisten ihrer Angehörigen – wohl eher ein eigenes Fach (vgl. Heckhausen 1987, S. 129–131) und eine Unterdisziplin der ← 7 | 8 → Germanistik, insofern sie sich auf fachbezogene Lehr-Lernprozesse des Schulfachs Deutsch bezieht. Die Frage, wie sie ihr Verhältnis zu ihren Bezugswissenschaften bestimmt – welche Perspektive sie also in ihren Fragestellungen priorisiert –, hat sich für die Deutschdidaktik immer gestellt, und sie ist innerhalb der Deutschdidaktik nie einheitlich beantwortet worden (vgl. z. B. Hurrelmann 1998; Rosebrock 2001; Winkler 2012; Kepser 2013). Die Öffnung für eine Zusammenarbeit mit anderen Fächern resp. Disziplinen erschien aber über lange Zeit kaum geboten, weil Forschende aus der Fachdidaktik Deutsch von ihrer Ausbildung und ihrem Selbstverständnis her Philologie und Pädagogik in Personalunion vertreten2, wenn auch mit jeweils individueller Akzentsetzung. Der Gegenstandsbereich der Deutschdidaktik ließ sich aus dieser Warte weitgehend autonom abdecken.
Die Wende zur Empirie und Kompetenzorientierung im Bildungswesen verunsicherte das fachliche Selbstverständnis der Fachdidaktik Deutsch3 – und zwar, obwohl sie zu diesem Zeitpunkt schon Erfahrungen in empirischer Forschung vorzuweisen hatte, wie Gerhard Rupp in seinem Überblicksbeitrag aufzeigt. Einschneidend für viele im Fach, insbesondere aus dem wissenschaftlichen Nachwuchs, war in diesem Zusammenhang die Forderung Norbert Groebens beim Symposion Deutschdidaktik 2004 in Lüneburg: Groeben hatte dafür plädiert, dass sich die Fachdidaktik Deutsch empirisch auszurichten habe, wenn sie nicht in der gesellschaftlichen wie wissenschaftlichen Bedeutungslosigkeit versinken wolle (vgl. Groeben 2005, S. 9). Ausgerufen wurde hier nicht weniger als die Notwendigkeit, durch eine Neuausrichtung die eigene fachliche Existenz zu legitimieren. Indem die Diskussion, wie es die Fachdidaktik mit der Empirie zu halten habe, diesem äußeren Rechtfertigungsdruck folgt, zeigt sie zum Teil eine „Tendenz ins Prinzipielle“ (Matuschek 2015, S.496), die fachliche Überlegungen über eine sinnvolle Ausdifferenzierung der Fachdidaktik in Richtung Empirie zurücktreten lässt.4
Aus der partiellen Empirisierung der Deutschdidaktik resultiert fachintern ein Spannungsverhältnis zwischen dem hermeneutisch-geisteswissenschaftlichen ← 8 | 9 → und dem empirisch-szientistischen Forschungsverständnis (vgl. Groeben 2006, S. 287). Folgt man Heckhausen (1987), dann konkurrieren damit innerhalb der Deutschdidaktik zwei „theoretische Integrationsniveau[s]“ (ebd., S. 132). Das theoretische Integrationsniveau ist es, das laut Heckhausen „die Disziplinarität eines Faches ausmacht“ (ebd.), weil es den wissenschaftstheoretischen Zugriff auf den ausgewählten Gegenstandsbereich und damit die Art und Weise regelt, wie „die betreffenden Sachverhalte der Wirklichkeit zu verstehen, zu erklären, vorherzusagen, praktisch zu nutzen, zu ändern“ (ebd.) sind. Das Verhältnis des hermeneutischen und empirischen Zugriffs auf deutschdidaktische Forschungsgegenstände konnte innerhalb des Faches nur teilweise produktiv geklärt werden.5 Gelingt dies nicht, entfremden sich Angehörige desselben Faches (vgl. dazu Frederking/Henschel, in diesem Band, S. 72).
Der vorliegende Sammelband nimmt Forschungszusammenhänge in den Blick, in denen die Fachdidaktik Deutsch über die Grenzen ihres Faches hinausschaut. Dies geschieht, wenn die eigene fachliche Spezialisierung und Ausdifferenzierung, die sich im Laufe der Zeit herausgebildet hat (vgl. Mittelstraß 1987, S. 153f.), nicht mehr ausreicht, um aktuelle Forschungsfragen zu untersuchen. Die nötige Perspektiverweiterung verlangt Aushandlungsprozesse mit Forschenden aus anderen Wissenschaftsgebieten, d. h. die Verständigung mit mehr oder weniger ‚fremden Schwestern‘. Im Folgenden werden also solche Projekte vorgestellt, in denen die Deutschdidaktik mit anderen Fächern resp. Disziplinen kooperiert, um Forschungs- und Entwicklungsfragen zu lösen, die die Deutschdidaktik in hohem Maß betreffen, aber nicht von ihr allein zu bearbeiten sind. Als Merkmal von Interdisziplinarität reicht dabei die Kooperation nicht aus (Klein 2010, S. 19). Vielmehr geht es im Kern um die Synthese unterschiedlicher fachlicher Perspektiven mit Blick auf eine gemeinsame Problemstellung („Learning to synthesize“, vgl. Boix Mansilla 2010). Die Integration und Interaktion der einzelnen fachlichen Perspektiven kann dabei graduell sehr unterschiedlich ausgeprägt sein (vgl. Klein 2010), wie sich auch in den folgenden Beiträgen zeigt.
2 Konstellationen und Zielrichtungen
Bereits Heckhausen (1972, S. 87–89) hat in einem viel zitierten Beitrag verschiedene Abstufungen („stage[s] of maturity“, ebd., S. 87) der interdisziplinären Zusammenarbeit unterschieden. Seine Unterscheidung greifen wir auf, wenn wir die in diesem Band vorgestellten Projekte in ein zweidimensionales Modell interdisziplinärer Forschung einordnen (Abb. 1). Zum einen werden die einzelnen Forschungsprojekte ← 9 | 10 → entlang einer Achse zunehmender Interaktion und Integration fachlicher Perspektiven unterschieden. Für diese Achse verwenden wir hier den Begriff Synthesegrad. Unter Synthese verstehen wir das übergreifende Forschungsergebnis, in dem wissenschaftliche Erkenntnisse und methodische Ansätze der beteiligten Fächer bzw. Disziplinen zusammengeführt werden (vgl. Defila/Di Giulio 2015, S. 125f.), so dass im weitreichendsten Fall aus dieser Integration etwas qualitativ Neues entsteht. Die zweite Achse unseres Modells fokussiert das primäre Erkenntnisinteresse interdisziplinärer Projekte, also ob die zu klärende Fragestellung aus gesellschaftlichen Problemen bzw. Anforderungssituationen resultiert oder aus der Wissenschaft selbst stammt. Damit knüpfen wir u. a. an Überlegungen von Mittelstraß (2005) an, der seinerseits Forschungsprojekte nach praktischer und theoretischer Ausrichtung interdisziplinärer Zusammenarbeit6 differenziert. Erstere greift außerwissenschaftliche Problemstellungen, also konkrete Notwendigkeiten verschiedener Handlungsfelder, auf; letztere setzt sich mit Problemen auseinander, die in der Wissenschaft selbst aufgeworfen werden.7
Abb. 1: Modell interdisziplinärer Forschung
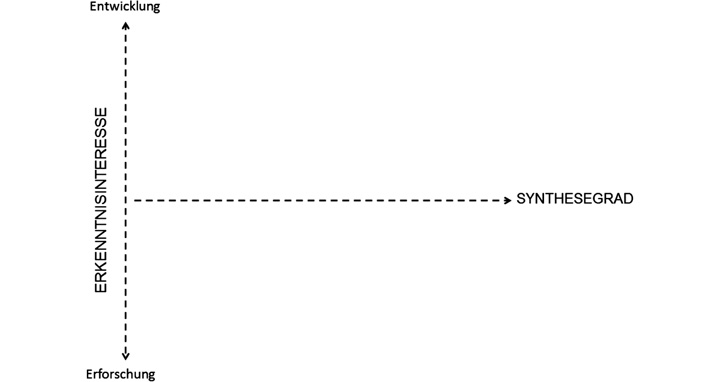
Man kann diskutieren, ob Forschung, an der die Deutschdidaktik beteiligt ist, nicht stets praktische Relevanz für ihren Gegenstandsbereich, den Deutschunterricht, beanspruchen muss (vgl. z. B. Ossner 1993, 1999) und die getroffene Unterscheidung von diesem Hintergrund obsolet ist. Sicher handelt es sich auch hier weniger um eine dichotome als um eine graduelle Differenz. Wir meinen an den Projekten, die in diesem Band vorgestellt werden, zu erkennen, dass der Anstoß für die interdisziplinäre Kooperation mal mehr, mal weniger von Entwicklungsbedarfen der Schulpraxis bzw. der Bildungsadministration getragen oder auf diese ausgerichtet ist (Abb. 2). Eine eigene Variante interdisziplinärer Forschung bilden dabei diejenigen Projekte, in die Mitwirkende aus der außerwissenschaftlichen Praxis einbezogen sind (Behrens/Weirich; Böhme/Stanat/Becker-Mrotzek; Lindauer et al.; Pieper/Sâmihăian).8
Da sie von der Anlage der Zusammenarbeit her über die Wissenschaft hinaus gehen, können sie mit Defila/Di Giulio (1999) als transdisziplinär bezeichnet werden – eine Bezeichnung, die Thomas Lindauer, Claudia Schmellentin und Anne Beerenwinkel in ihrem Beitrag aufnehmen. Ob diese Projekte eher ‚praktisch‘ oder ‚theoretisch‘ ausgerichtet sind, hängt allerdings nicht allein von der Einbeziehung von Beteiligten des nicht-akademischen Handlungsfeldes ab.
Abb. 2: Einordnung der Projekte in diesem Band in das Modell interdisziplinärer Forschung
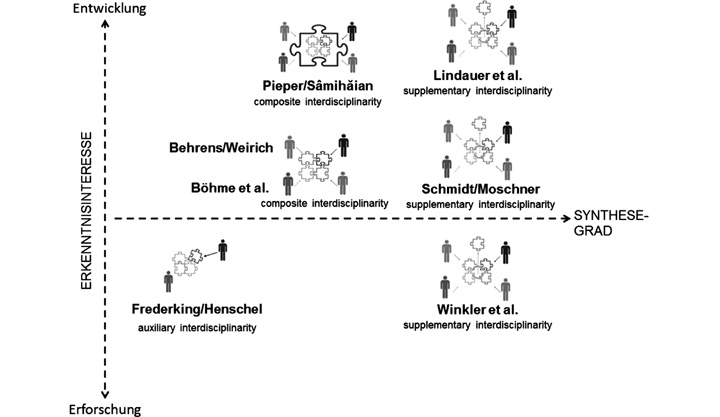
2.1 Erkenntnisinteresse der interdisziplinären Zusammenarbeit: Entwicklungs- oder Forschungsorientierung
Einige der im skizzierten Sinn ‚transdisziplinären’ Projekte greifen explizit Entwicklungsbedarfe außerwissenschaftlicher Handlungsfelder auf (vgl. Abb. 2). So zeigen Ulrike Behrens und Sebastian Weirich, wie sich das Projekt stim·mig der virulenten Anforderung stellt, geeignete Aufgabenstellungen für die Überprüfung von Zuhörkompetenz zu konstruieren. Im Rahmen des Projekts Fachlernen und Sprache (Lindauer et al., in diesem Band) werden Materialien und Handreichungen für einen sprachbewussten Fachunterricht entwickelt. Auch das Projekt LIFT folgt einem Entwicklungsziel, das am professionellen Bedarf von Literaturlehrerinnen und -lehrern in Europa ausgerichtet ist und deren Perspektive bereits in der Anlage des Projektes mit einbezieht, wie Irene Pieper und Florentina Sâmihăian in ihrem Beitrag deutlich machen.
Eine Zwischenstellung zwischen Erforschung und Entwicklung nehmen die Projekte ein, die Katrin Böhme, Petra Stanat und Michael Becker-Mrotzek sowie Frederike Schmidt und Barbara Moschner vorstellen. Katrin Böhme et al. geht es im Kontext der KMK-Bildungsstandards darum, empirisch fundierte integrierte Kompetenzstufenmodelle aufzustellen. „Die Entwicklung solcher Kompetenzstufenmodelle erfolgt immer in einem Abstimmungsprozess zwischen Wissenschaft, Schulpraxis und Bildungspolitik“ (Böhme et al., in diesem Band, S. 112). Der Auftrag für diese Entwicklung kommt explizit aus der Bildungspolitik. Entsprechende domänenspezifische Kompetenzstufenmodelle sind aber zugleich auch ein Forschungsdesiderat der Fachdidaktik, wenn sie die mit der Kompetenzorientierung verbundenen wissenschaftlichen Herausforderungen ernst nimmt. Das Promotionsprogramm ProfaS, das im Zentrum des Beitrags von Schmidt und Moschner steht, ist als Forschungsprogramm mit empirischer Ausrichtung konzipiert. Von seinem theoretischen Rahmen her zielt es gleichwohl dezidiert auf die Entwicklung begründeter Leitlinien für die Lehrerbildung.
Im Projekt LUK, das Volker Frederking und Sofie Henschel in ihrem Beitrag beleuchten, steht eine zunächst vorwiegend wissenschaftsgeleitete Fragestellung im Zentrum, nämlich die theoretische Klärung und empirische Validierung des Konstrukts „Literarästhetische Textverstehenskompetenz“. Auch das Projekt von Iris Winkler, Matthias Heinrich, Astrid Fischer und Ulrike Krause verfolgt in erster Linie das Forschungsziel, die Wirkung von Multiperspektivität in fachdidaktischen Lernumgebungen zu untersuchen. Dass die genannten Klärungen auf längere Sicht für das Anwendungsfeld relevant sein können und sogar sollen, ist von der getroffenen Einordnung nach dem primären Erkenntnisinteresse der interdisziplinären Zusammenarbeit unbenommen. ← 12 | 13 →
2.2 Synthesegrade interdisziplinärer Forschung
Die vorgestellten Projekte zeigen, dass in der interdisziplinären Kooperation die beteiligten fachlichen Perspektiven und Wissensbestände graduell unterschiedlich synthetisiert werden. In Anknüpfung an Heckhausen (1972, S. 87–89) sehen wir folgende Synthesegrade9 repräsentiert:
Auxiliary Interdisciplinarity: Die kooperierenden Fächer resp. Disziplinen bedienen sich wechselseitig der methodischen Expertise oder des fachlichen Wissens des Partners, um Lücken zu schließen, die aus der eigenen Spezialisierung resultieren. Ausgangs- und Zielgröße der Zusammenarbeit ist die eigene Disziplin. Ein Beispiel hierfür ist das Projekt LUK (Frederking/Henschel, in diesem Band).10 Die Einbeziehung von Wissensbeständen und methodischen Zugangsweisen der anderen Disziplin(en) ist also eher auf Kompensation als auf Integration und Synthese ausgerichtet.
Composite Interdisciplinarity: In diesen Projekten, die i. d. R. transdisziplinär im obigen Sinn angelegt sind, ist zum Erreichen des gemeinsamen Ziels die Kombination verschiedener Perspektiven erforderlich, die sich zu einem Ganzen ergänzen („jigsaw puzzle-like composition“, Heckhausen 1972, S. 88). Die beteiligten Disziplinen teilen streng genommen nicht einmal denselben Gegenstandsbereich noch dasselbe theoretische Integrationsniveau. Einzig die Erfordernisse der spezifischen ← 13 | 14 → Problemstellung verbinden die Partner. Diese Konstellation sehen wir im Projekt stim·mig (Behrens/Weirich), im Projekt LIFT-211 und bei der Entwicklung integrierter Kompetenzstufenmodelle am IQB (Böhme et al.) gegeben. Heckhausen (1987, S. 138) betont zwar, dass die kombinierten Perspektiven und Wissensbestände bei dieser Variante der Interdisziplinarität nebeneinander stehen bleiben – in diesem Sinn käme es nicht zur weiterführenden Synthese. Unseres Erachtens sind aber Wechselwirkungen zwischen den Perspektiven im Prozessverlauf als Begleiteffekt durchaus erwartbar. Entsprechend heben z. B. Behrens und Weirich in ihrem Beitrag hervor, dass ein
wesentliches Charakteristikum solcher interdisziplinären Projekte ist, dass die Perspektiven nicht mehr einzelnen Personen(-gruppen) strikt zugeordnet werden können. Vielmehr ergibt sich im gemeinsamen Arbeitsprozess erkennbar eine gegenseitige Qualifikation aller Beteiligten. (Behrens/Weirich, in diesem Band, S. 150)
Damit ist bereits ein fließender Übergang zur nächsten Synthesestufe interdisziplinärer Zusammenarbeit markiert.
Details
- Seiten
- 246
- Erscheinungsjahr
- 2016
- ISBN (Hardcover)
- 9783631663400
- ISBN (ePUB)
- 9783631692851
- ISBN (MOBI)
- 9783631692868
- ISBN (PDF)
- 9783653056655
- DOI
- 10.3726/978-3-653-05665-5
- Open Access
- CC-BY-NC-ND
- Sprache
- Deutsch
- Erscheinungsdatum
- 2016 (August)
- Erschienen
- Frankfurt am Main, Berlin, Bern, Bruxelles, New York, Oxford, Wien, 2016. 246 S., 16 s/w Abb., 6 s/w Tab.
- Produktsicherheit
- Peter Lang Group AG

