Lógos and Máthēma 2
Studies in the Philosophy of Logic and Mathematics
Summary
Excerpt
Table Of Contents
- Cover
- Title Page
- Copyright
- Dedication
- Foreword
- Contents
- On the Philosophical Meaning of Reverse Mathematics
- On the Distinction Proof–Truth in Mathematics
- Some Historical, Philosophical and Methodological Remarks on Proof in Mathematics
- The Status of Church’s Thesis (co-author: Jan Woleński)
- Between Theology and Mathematics. Nicholas of Cusa’s Philosophy of Mathematics
- Phenomenological Ideas in the Philosophy of Mathematics. From Husserl to Gödel (co-author: Thomas Bedürftig)
- Mathematical Foundations and Logic in Reborn Poland
- Tarski and his Polish Predecessors on Truth (co-author: Jan Woleński)
- Benedykt Bornstein’s Philosophy of Logic and Mathematics
- Philosophy of Logic and Mathematics in the Warsaw School of Mathematical Logic
- The philosophy of Mathematics and Logic in Cracow between the Wars
- Philosophy of Logic and Mathematics in the Lvov School of Mathematics
- Cracow Circle and Its Philosophy of Logic and Mathematics
- Bibliography
- Source Note
- Index
On the Philosophical Meaning of Reverse Mathematics
The aim of this chapter is to discuss the meaning of some recent results in the foundations of mathematics – more exactly of the so-called reverse mathematics – for the philosophy of mathematics. In particular, we shall be interested in implications of those results for Hilbert’s program.
Hilbert’s program
One of the reactions on the crisis in the foundations of mathematics on the turn of the 19th century was Hilbert’s program. Hilbert’s aim was to save the integrity of classical mathematics (dealingwith actual infinity) by showing that it is secure.1 He saw also the supra-mathematical significance of this issue. In 1926 he wrote: “The definite clarification of the nature of the infinite has become necessary, not merely for the special interests of the individual sciences, but for the honor of human understanding itself ”. Being first of all a mathematician, he “had little patience with philosophy, his own philosophy of mathematics being perhaps best described as naïve optimism – a faith in the mathematician’s ability to solve any problem he might set for himself ” (cf. Smoryński 1988).
Hilbert’s program of clarification and justification of mathematics was Kantian in character (cf. Detlefsen 1993). Following Kant, he claimed that the mathematician’s infinity does not correspond to anything in the physical world, that it is “an idea of pure reason” – as Kant used to say. On the other hand, Hilbert wrote in (1926):
Kant taught – and it is an integral part of his doctrine – that mathematics treats a subject matter which is given independently of logic. Mathematics, therefore can never be grounded solely on logic. Consequently, Frege’s and Dedekind’s attempts to so ground it were doomed to failure.
As a further precondition for using logical deduction and carrying out logical operations, something must be given in conception, viz., certain extralogical concrete objects which are intuited as directly experienced prior to all thinking. For logical deduction to be certain, we must be able to see every aspect of these objects, and their properties, differences, sequences, and contiguities must be given, together with the objects themselves, as ←11 | 12→something which cannot be reduced to something else and which requires no reduction. This is the basic philosophy which I find necessary not just for mathematics, but for all scientific thinking, understanding and communicating. The subject matter of mathematics is, in accordance with this theory, the concrete symbols themselves whose structure is immediately clear and recognizable.2
According to this, Hilbert distinguished between the unproblematic, finitistic part of mathematics and the infinitistic part which needed justification. Finitistic mathematics deals with so-called real sentences, which are completely meaningful because they refer only to given concrete objects. Infinitistic mathematics on the other hand deals with so-called ideal sentences that contain reference to infinite totalities. Hilbert believed that every true finitary proposition had a finitary proof. Infinitistic objects and methods played only an auxiliary role. They enabled us to give easier, shorter and more elegant proofs but every such proof could be replaced by a finitary one. He was convinced that consistency implies existence and that every proof of existence not giving a construction of postulated objects is in fact a presage of such a construction.
Unfortunately, Hilbert did not give a precise definition of finitism – one finds by him only some hints how to understand it. Hence various interpretations are possible (cf., e.g. Detlefsen 1979; Prawitz 1983; Resnik 1974; Smorynski 1988; Tait 1981).
The infinitistic mathematics can be justified only by finitistic methods because only they can give it security (Sicherheit). Hilbert’s proposal was to base mathematics on finitistic mathematics via proof theory. Its main goal was to show that proofs which use ideal elements in order to prove results in the real part of mathematics always yield correct results. We can distinguish here two aspects: consistency ←12 | 13→problem and conservation problem3.The former consists in showing (by finitistic methods) that the infinitistic mathematics is consistent, and the latter – in showing (again by finitistic methods) that any real sentence which can be proved in the infinitistic part of mathematics can be proved also in the finitistic part, i.e. that infinitistic mathematics is conservative over finitistic mathematics with respect to real sentences and, even more, that there is a finitistic method of translating infinitistic proofs of real sentences into finitistic ones.4
Hilbert wanted to solve those problems via his proof theory. His proposal to carry out the program consisted of two steps: 1. to formalize mathematics, i.e., to reconstruct infinitistic mathematics as a big, elaborate formal system and 2. to give a proof of the consistency and conservativeness of mathematics. It should be done by finitistic methods, and it was possible since after formalization one could treat formulas of the system of mathematics as strings of symbols and proofs as strings of formulas (i.e., as strings of strings of symbols).
Incompleteness results
Hilbert and his school had scored some successes in realization of the program of justification of infinite mathematics. In particular, Hilbert’s student W. Ackermann showed by finitistic methods the consistency of a fragment of arithmetic of natural numbers (cf. Ackermann 1924–1925, 1940). But soon, something was to happen that undermined Hilbert’s program.
We mean here the incompleteness results of Gödel from 1930 which indicated certain cognitive limitations of the deductive methods (cf. Gödel 1931). They showed that one cannot include the whole mathematics in a consistent formalized system based on the first order predicate calculus – what more, one cannot even include in such a system all truth about natural numbers. Even more, no formal theory containing arithmetic of natural numbers can prove its own consistency.
Gödel’s results struck Hilbert’s program. The question whether they rejected it cannot be answered definitely. The reason is that Hilbert’s program was not formulated precisely enough. Hence, various opinions are formulated and defended (cf., e.g. Detlefsen 1979, 1990; Resnik 1974; Smorynski 1977, 1985, 1988). But one thing ←13 | 14→should be stressed here: the failure of Hilbert’s programme for a certain formalized system of arithmetic need not be a failure of Hilbert’s programme for elementary number theory in the informal sense. In fact, one cannot exclude the possibility that the latter can be formalized in a system which can be justified on finitistic grounds.5
Gödel’s true but undecidable (in the formal system of arithmetic) sentence had not mathematical but in fact metamathematical contents (it states: “I am not a theorem”). This diminished the meaning and significance of Gödel’s results. There arose a question: Is it possible to indicate examples of true undecidable sentences of mathematical, in particular number–theoretical, contents? Or formal mathematics is complete with respect to sentences which are interesting and reasonable from the mathematical point of view (whatever it means)?
These questions were answered by J. Paris, L. Harrington and L. Kirby who gave examples of true undecidable sentences of combinatorial contents (cf. Paris and Harrington 1977) and of number–theoretical contents (cf. Kirby, Paris 1982). They are examples of true arithmetical sentences without “pure”, i.e., arithmetical proofs. More exactly, we got sentences talking about some combinatorial properties of finite sets or properties of sequences of natural numbers but natural proofs of them use infinite sets and, since they cannot be proved in Peanoarithmetic PA, each such proof must contain something from beyond the domain of finite objects. Thus they are theorems having “impure” but no “pure” proofs.
Add that those results were used by quasi-empiricists in mathematics who argue that mathematics is not an a priori knowledge, it is not absolute and certain, but is rather quasi-empirical, probable and fallible; mathematics is in fact similar to natural sciences. The new undecidable results indicate also that, as E. Post put it, “mathematical proof is in fact a result of creative activity of reason”, it is impossible to bound a priori the invention of a mathematician.
←14 | 15→Generalized Hilbert’s program
The natural consequence of incompleteness results was the idea of extending the admissible methods and allowing general constructive methods instead of finitistic ones only6. This led to the generalized Hilbert’s program.
Though the concept of general constructive methods is unprecise, still the idea of broadening of original Hilbert’s proof theory has become an accepted paradigm. Investigations were carried out in this direction, and several results were obtained (cf. Feferman 1988; Feferman 1964–1968; Gödel 1958; Kreisel 1958; Schütte 1977; Simpson 1985; Takeuti 1987). We want to note here only that they led to two surprising insights: (a) classical analysis can be formally developed in conservative extensions of elementary number theory and (b) strong impredicative subsystems of analysis can be reduced to constructively meaningful theories, i.e., relative consistency proofs can be given by constructive means for impredicative parts of second order arithmetic.
On the other hand, it should be stressed that all the proposed generalizations of Hilbert’s program, are in fact very different from the original Hilbert’s proposal. Hilbert’s postulate was the validation and justification of classical mathematics by a reduction to finitistic mathematics. The latter was important here for philosophical and, say, ideological reasons: finitistic objects and reasonings have clear physical meaning and are indispensable for all scientific thought. None of the proposed generalizations can be viewed as finitistic (whatever it means). Hence they have another value and meaning from the methodological and generally philosophical point of view. They are not contributing directly to Hilbert’s program, but on the other hand they are in our opinion compatible with Hilbert’s reductionist philosophy.
Reverse mathematics vs. Hilbert’s program
Another consequence of incompleteness results (besides those described above) is so-called relativized Hilbert’s program. If the entire infinitistic mathematics cannot be reduced to and justified by finitistic mathematics then one can ask for which part of it is that possible? In other words:Howmuch of infinitistic mathematics can ←15 | 16→be developed within formal systems which are conservative over finitistic mathematics with respect to real sentences? This constitutes the relativized version of Hilbert’s program. In what follows, we would like to show how the so-called reverse mathematics of Friedman and Simpson contributes to it, providing us with a partial realization of Hilbert’s original program.
To be able to consider the issue we should first specify what is exactly meant by finitistic mathematics and by real sentences. We shall follow Tait (1981) where it is claimed that Hilbert’s finitism is captured by the formal system of primitive recursive arithmetic7 (PRA, also called Skolem arithmetic). By real sentences we shall mean Πsentences of the language of Peano arithmetic PA.
It turns out that one can formalize classical mathematics not only in set theory, but most of its parts (such as geometry, number theory, analysis, differential equations, complex analysis, etc.) can be formalized in a weaker system called second order arithmetic 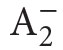 (denoted also sometimes by Z2).8 This is a system formalized in a language
(denoted also sometimes by Z2).8 This is a system formalized in a language 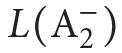 with two sorts of variables: number variables x, y, z, . . . and set variables X,Y,Z, . . . Its nonlogical constants are those of Peano arithmetic PA, i.e., o,S,+,⋅ and the membership relation ∈. Nonlogical axioms of
with two sorts of variables: number variables x, y, z, . . . and set variables X,Y,Z, . . . Its nonlogical constants are those of Peano arithmetic PA, i.e., o,S,+,⋅ and the membership relation ∈. Nonlogical axioms of 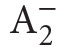 are the following:
are the following:
- axioms of PA without the axiom scheme of induction,
- (extensionality)
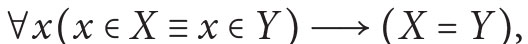
- (induction axiom)

- (axiom scheme of comprehension)
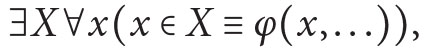 where φ(x, . . .) is any formula of the language
where φ(x, . . .) is any formula of the language 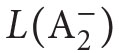 (possiblywith free number-or set-variables) in which X does not occur free.
(possiblywith free number-or set-variables) in which X does not occur free.
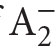 are structures of the form (X ,M,∈) where Mis a model of PA and X is a family of subsets of the universe of the model M. (More information on
are structures of the form (X ,M,∈) where Mis a model of PA and X is a family of subsets of the universe of the model M. (More information on 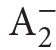 and its models can be found in Apt, Marek (1974), and Murawski (1976–1977, 1984a).)
and its models can be found in Apt, Marek (1974), and Murawski (1976–1977, 1984a).)Second order arithmetic is a nice system because one avoids here troubles connected with set theory (in which mathematics is usually formalized), and on the other hand it is strong enough to provemany important theorems of classical mathematics. There is only a problem of impredicativity9 of 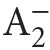 (connected with the axiom scheme of comprehension, where φ may be any formula of the language of ←16 | 17→
(connected with the axiom scheme of comprehension, where φ may be any formula of the language of ←16 | 17→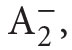 hence in particular φ may be of the form ∀Yψ(Y, x, . . .)). But it turns out that in many cases certain fragments of
hence in particular φ may be of the form ∀Yψ(Y, x, . . .)). But it turns out that in many cases certain fragments of 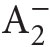 suffice, i.e., only particular special forms of the comprehension axiom are needed.
suffice, i.e., only particular special forms of the comprehension axiom are needed.
At the Congress of Mathematicians in Vancouver in 1974 H.Friedman formulated a program of foundations of mathematics called today “reversemathematics” (cf. Friedman 1975). Its aim is to study the role of set existence axioms, i.e., comprehension axioms in ordinary mathematics. The main problem is: Given a specific theorem τ of ordinary mathematics, which set existence axioms are needed in order to prove τ? This research program turned out to be very fruitful and led to many interesting results.10
The procedure used in the reverse mathematics (it reveals the inspiration for its name) is the following: Assume we know that a given theorem τ can be proved in a particular fragment S(τ) of 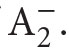 Is S(τ) the weakest fragment with this property? To answer this question positively, one shows that the principal set existence axiom of S(τ) is equivalent to τ, the equivalence being provable in some weaker system in which τ itself is not provable. Thus reverse mathematics is, from the point of view of the philosophy of mathematics, an example of a reductionist program with a firm mathematical basis.
Is S(τ) the weakest fragment with this property? To answer this question positively, one shows that the principal set existence axiom of S(τ) is equivalent to τ, the equivalence being provable in some weaker system in which τ itself is not provable. Thus reverse mathematics is, from the point of view of the philosophy of mathematics, an example of a reductionist program with a firm mathematical basis.
Some specific systems – fragments of 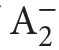 – arose in this context; the most important are: RCA0,WKL0, ACA0, ATRo and
– arose in this context; the most important are: RCA0,WKL0, ACA0, ATRo and 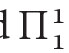 −CA.We shall describe only the first three of them.
−CA.We shall describe only the first three of them.
The system RCA0 is a theory in the language of 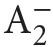 based on the following axioms: (i) PA− (i.e., axioms of Peano arithmetic PA without the axiom scheme of induction), (ii) scheme of induction for
based on the following axioms: (i) PA− (i.e., axioms of Peano arithmetic PA without the axiom scheme of induction), (ii) scheme of induction for 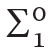 formulas,11 i.e.:
formulas,11 i.e.:
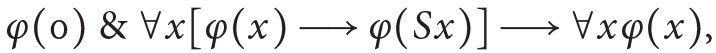
where φ is a 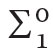 formula, (iii) (recursive comprehension axiom)
formula, (iii) (recursive comprehension axiom)
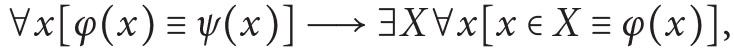
where φ is 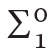 and ψ is
and ψ is 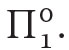 [Axiom (iii) explains the name RCA0 of the theory.] It can be shown that (Rec,N,∈), where No is the standard model of Peano arithmetic PA and Rec is the family of all recursive sets, is a model of RCA0.
[Axiom (iii) explains the name RCA0 of the theory.] It can be shown that (Rec,N,∈), where No is the standard model of Peano arithmetic PA and Rec is the family of all recursive sets, is a model of RCA0.
The theory WKL0 consists of RCA0 plus a further axiom known as weak König’s lemma (therefore the name WKL0) which states that every infinite binary tree has an infinite path (this can be formulated in the language of 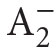 using coding). It is ←17 | 18→stronger than RCA0 what follows, e.g. from the fact that (Rec,N,∈) is not a model of WKL0 (this is a consequence of Gödel’s theorem on essential undecidability of Peano arithmetic).
using coding). It is ←17 | 18→stronger than RCA0 what follows, e.g. from the fact that (Rec,N,∈) is not a model of WKL0 (this is a consequence of Gödel’s theorem on essential undecidability of Peano arithmetic).
Details
- Pages
- 224
- Publication Year
- 2020
- ISBN (Hardcover)
- 9783631807149
- ISBN (PDF)
- 9783631820186
- ISBN (ePUB)
- 9783631820193
- ISBN (MOBI)
- 9783631820209
- DOI
- 10.3726/b16869
- Language
- English
- Publication date
- 2020 (April)
- Published
- Berlin, Bern, Bruxelles, New York, Oxford, Warszawa, Wien, 2020. 224 pp.
- Product Safety
- Peter Lang Group AG

