Volatility as an Asset Class
Obvious Benefits and Hidden Risks
Summary
Excerpt
Table Of Contents
- Cover
- Title
- Copyright
- About the author(s)/editor(s)
- About the book
- This eBook can be cited
- Contents
- Introduction
- 1 Volatility and Its Estimation
- 1.1 Introduction
- 1.2 Volatility measurement
- 1.2.1 Alternative volatility estimators
- 1.2.2 High-frequency data
- 1.2.3 Concluding remarks
- 1.3 Volatility forecasting
- 1.3.1 Time series analysis
- 1.3.2 Forecasts implied by option prices
- 1.3.3 Concluding remarks
- 1.4 Volatility surface and option pricing
- 1.4.1 Local volatility model
- 1.4.2 Stochastic volatility models
- 1.4.3 Concluding remarks
- 1.5 Conclusions
- 2 Overview of volatility derivatives
- 2.1 Volatility exposure in a delta-hedged option
- 2.2 Variance swaps
- 2.3 VIX and VIX futures
- 2.4 VIX options
- 2.5 The economics of volatility derivatives
- 3 Options Delta Hedging with No Options at All
- 3.1 Introduction
- 3.2 Options as volatility instruments – replicating realized volatility
- 3.3 Volatility arbitrage based on various frequencies of data
- 3.4 Methodology and data
- 3.5 Empirical research
- 3.5.1 S&P500 index – the most developed market
- 3.5.2 The case for other developed markets (FTSE, NIKKEI225, DAX)
- 3.5.3 The case for emerging markets (WIG20, KOSPI, BOVESPA) ...
- 3.6 Summary
- 4 Volatility Derivatives in Portfolio Optimization
- 4.1 Introduction
- 4.2 The merits of investing in volatility
- 4.3 Volatility in portfolio optimization
- 4.3.1 Benchmark portfolio
- 4.3.2 Long position in implied volatility
- 4.3.3 Short position in realized volatility
- 4.3.4 A combination of long and short position in volatility
- 4.4 Summary
- 5 Benefits of Using Volatility Futures in Investment Strategies
- 5.1 Introduction
- 5.2 Volatility as a traded asset
- 5.3 Markowitz model – a short review 101
- 5.4 Black-Littermann model – a short review
- 5.5 Markowitz model – application
- 5.5.1 Data used
- 5.5.2 Simulation
- 5.5.3 Empirical results
- 5.6 Black-Litterman model – application
- 5.6.1 Data used
- 5.6.2 Simulation
- 5.6.3 Empirical results
- 5.7 Summary
- 6 Predictive Properties of the Volatility Term Structure
- 6.1 Introduction
- 6.2 Volatility term structure of VIX futures – predictive properties based on regression model
- 6.2.1 Motivation
- 6.2.2 Literature review
- 6.2.3 Methodology and data
- 6.2.4 Results
- 6.2.5 Remarks
- 6.3 Predicting VIX – an investment model approach
- 6.3.1 Motivation
- 6.3.2 Data description
- 6.3.3 Methodology
- 6.3.4 Measures of volatility term structure
- 6.3.5 Forecasting properties of volatility term structure
- 6.3.6 Investment model
- 6.4 Summary
- Conclusions
- List of figures
- List of tables
- Bibliography
| 9 →
This book presents some practical aspects of a relatively novel asset class – volatility1. We believe that there is no need to argue that volatility does constitute a new asset class. The reason for this is not only that the number of standard volatility derivatives has been steadily growing since the mid-2000s but more importantly a constant development of the huge number of more complex derivatives through which investors can gain indirect exposure to various types of volatility.
Initially, trading volatility meant trading futures (2004) and options (2006) contracts written on the VIX. Then VSTOXX index futures were introduced by EUREX in 2009 and after a few years VSTOXX index options as well2. Later on, the large group of VIX exchange-traded products was proposed by Barclays Bank, which also was the first institution to issue notes on the S&P 500 VIX Short-Term and Mid-Term total return futures indexes in 2009. Currently, ETF Database shows 16 US – traded ETFs in the volatility category3. Additionally, there is a wide range of volatility derivatives beyond these based on VIX index. Some of them are listed below:
1. VXEWZ, OVX, GVZ, VXN, RVX, VXST, VXEEM and VXTYN index futures quoted on CFE exchange: http://www.cboe.com/micro/volatility/introduction.aspx
2. VNKY index futures quoted on OSAKA exchange: http://www.ose.or.jp/e/
3. VHSI index futures quoted on Hong Kong exchange: http://www.hkex.com.hk/eng/index.htm
4. India VIX index futures quoted on NSE: http://www.nseindia.com/live_market/dynaContent/live_watch/vix_home_page.htm
5. S&P/ASX200 VIX index futures quoted on ASX: http://www.asx.com.au/index.htm ← 9 | 10 →
6. RVI index futures quoted on Moscow Exchange: http://moex.com/s381
7. VKOSPI index futures quoted on KRX: http://eng.krx.co.kr/m1/m1_4/m1_4_4/m1_4_4_3/UHPENG01004_04_03.html
Some of these instruments represent a growing market of substantial size. VIX derivatives are the most important segment of volatility derivatives. There is a steady growth in trading volume in VIX futures markets since 2008. Currently, a 12-month average of monthly trading volume is approximately 4 million of contracts traded per month (Figure 0.0.1). When we consider open interest in the VIX market the situation is slightly different. It raised significantly between 2009 and 2012 but stabilized at the level of 0.4 million since 2013 (Figure 0.0.1). VSTOXX futures traded on Eurex Group achieved the record level of 1 milion contracts per month in 2014 (October 2014). These contracts are currently the second most heavily exchange-traded volatility futures worldwide. Detailed data describing trading volume and open interest with their 12-month average values are presented in Figure 0.0.2. Trading volume of VSTOXX futures shows that these contracts have been growing steadily since 2009. Currently, 12-month average of monthly trading volume is at the level of 0.5 million of contracts traded per month4 (Figure 0.0.2). When we consider open interest the situation for VSTOXX futures is once again similar to VIX futures. It went up significantly between 2009 and 2012 but stabilized at the level of 0.2 mn open interest since 2013.5 ← 10 | 11 →
Figure 0.0.1: VIX index futures fluctuations, trading volume and open interest statistics
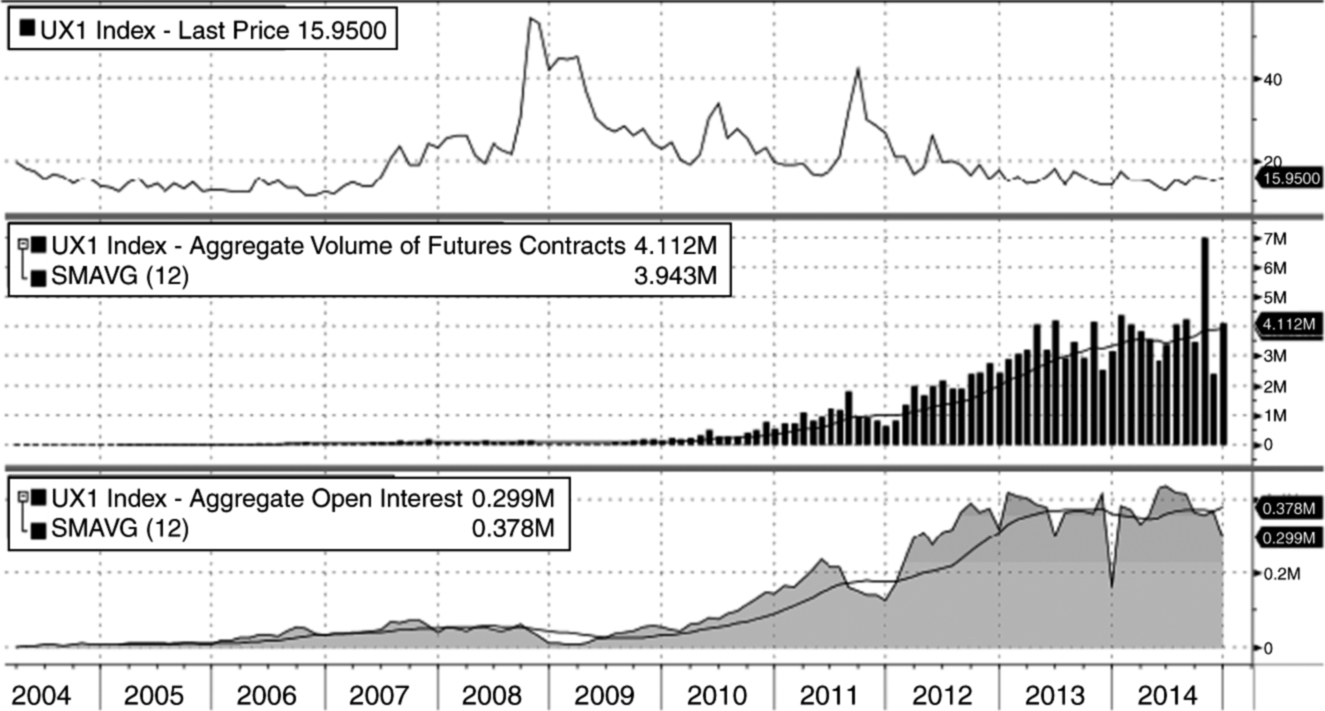
Note: Monthly data cover the period between 2004–2014. The top panel shows VIX future fluctuations. The middle panel shows monthly trading volume with 12-month average of monthly trading volume. The bottom panel presents monthly open interest and 12-month average of open interest.
Does observation concerning behaviour of open interest in 2013 and 2014 mean that two main exchange-traded volatility derivatives achieved some level of market saturation? The answer is not obvious as many other exchanges around the world try to introduce new exchange-traded volatility derivatives each year. The beginnings are rather difficult and volume data does not grow very fast because of many reasons. Therefore, markets in other volatility derivatives, mentioned in the earlier list, are much smaller than those of VIX and VSTOXX derivatives6. On the other hand, CFTC data show that in mid-2014 total value of variance swap outstanding (for S&P 500, Eurostoxx 50, Russell 2000, FTSE 100, Nikkei 225, Kospi 200 and others) went over USD 2 billion vega (Mixon and Onur (2014)). Thus, there is a very limited number of markets in volatility derivatives that may be perceived as mature market. On the other hand, there is a growing list of new instruments in this category with markets initially small and slowly growing. ← 11 | 12 →
Figure 0.0.2: VSTOXX index futures fluctuations, trading volume and open interest statistics
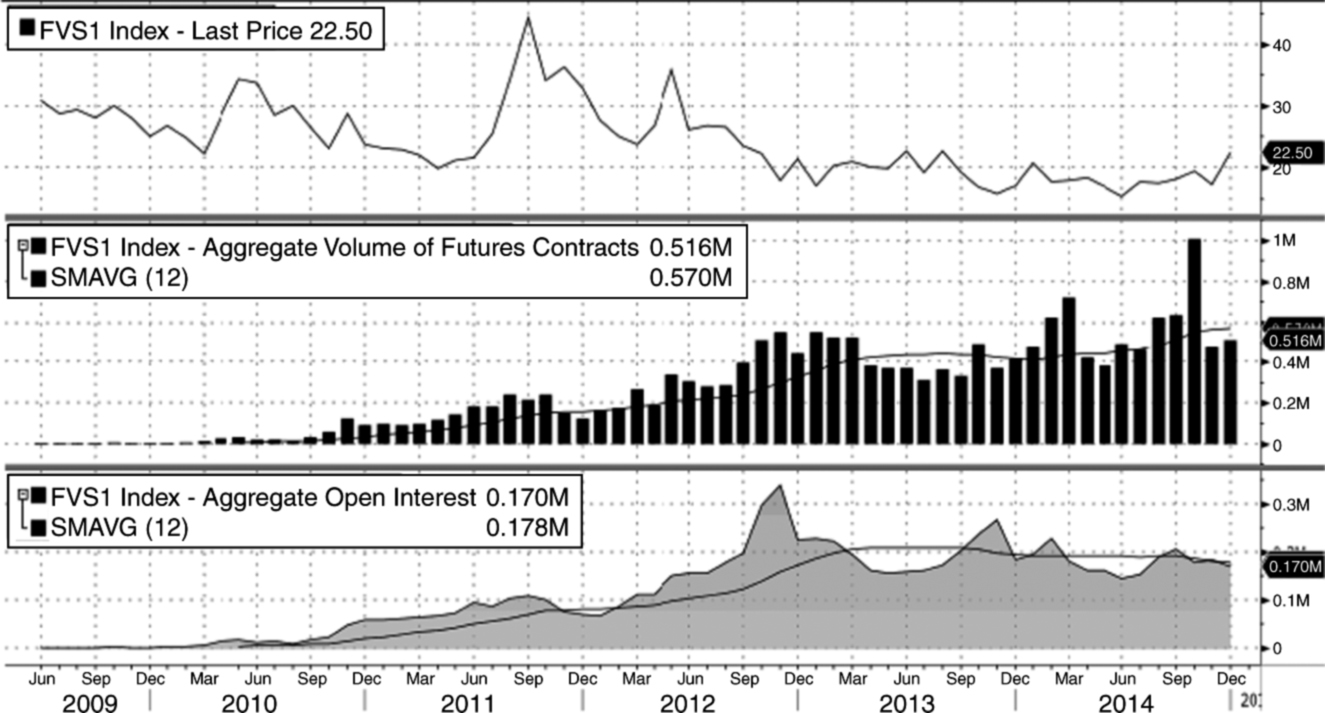
Note: Monthly data cover the period between 2009–2014. The top panel shows VSTOXX future fluctuations. The middle panel shows monthly trading volume with 12-month average of monthly trading volume. The bottom panel presents monthly open interest and 12-month average of open interest.
We hope that by presenting pros and cons of volatility trading we may introduce this new class of assets to a larger group of possible investors and contribute to further development of market in volatility derivatives. However, we think that the list of volatility instruments seems to be long enough to strongly support our belief that volatility is an asset class in itself. Hence, this book goes beyond this argument and its focus is fore-mostly an option pricing, volatility arbitrage strategies and an asset allocation context7. Statistical and econometric issues play only a secondary role here.
We begin in chapter 1 with an overview of methods for measuring, estimating, and modelling volatility. The existence of many surveys in this area, focusing on types of models applied for this purpose, motivated us to concentrate on the option pricing perspective. Nevertheless, we show in this chapter all major estimators of volatility and possible methods of forecasting its future fluctuations. We conclude this chapter with a section showing two model approaches to volatility forecasting that may also be used for option pricing consistent with market data, e.g. local volatility model and stochastic volatility models. ← 12 | 13 →
Details
- Pages
- 180
- Publication Year
- 2015
- ISBN (Softcover)
- 9783631655764
- ISBN (PDF)
- 9783653047875
- ISBN (MOBI)
- 9783653978834
- ISBN (ePUB)
- 9783653978841
- DOI
- 10.3726/978-3-653-04787-5
- Language
- English
- Publication date
- 2015 (April)
- Keywords
- Derivate Investitionsstrategien Portfolio Volatitlität
- Published
- Frankfurt am Main, Berlin, Bern, Bruxelles, New York, Oxford, Wien, 2015. 180 pp., 36 tables, 49 graphs
- Product Safety
- Peter Lang Group AG

